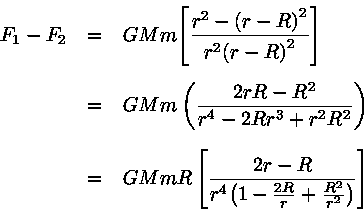|
 |
||||||||
| Lixo Recicle | Classificados | Astronomia | Desaparecidos | Noticias | Fale Conosco | |||
Corpos com simetria esférica agem, gravitacionalmente, como massas pontuais, para as quais as influências gravitacionais são facilmente calculadas. Na natureza, no entanto, os corpos na maioria das vezes não são perfeitamente esféricos. A principal contribuição à não esfericidade em planetas é a sua rotação. Outra contribuição é proporcionada pelas forças gravitacionais diferenciais que corpos vizinhos exercem uns nos outros. Essas forças diferenciais resultam em fenômenos como marés e precessão. A força total exercida sobre uma
partícula será:
A força gravitacional diferencial
é a diferença entre as forças gravitacionais exercidas em duas partículas
vizinhas por um terceiro corpo, mais distante. A figura abaixo ilustra a
força diferencial entre as partículas
Derivação da força diferencial
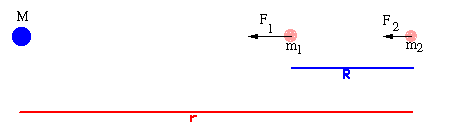
Considere as duas partículas da figura
acima. Chamemos de R a distância entre as duas partículas, e de
r a distância de M à partícula
Esta é a expressão da força diferencial dF na direção de dr. É basicamente a mesma expressão derivada acima, com a diferença de que aqui temos dr onde acima lá temos R. Isso nos diz portanto que dr é a separação entre os pontos para os quais estamos calculando a força diferencial. MarésAs marés na Terra constituem um fenômeno resultante da atração gravitacional exercida pela Lua sobre a Terra e, em menor escala, da atração gravitacional exercida pelo Sol sobre a Terra. A idéia básica da maré provocada pela Lua, por exemplo, é que a atração gravitacional sentida por cada ponto da Terra devido à Lua depende da distância do ponto à Lua. Portanto a atração gravitacional sentida no lado da Terra que está mais próximo da Lua é maior do que a sentida no centro da Terra, e a a atração gravitacional sentida no lado da Terra que está mais distante da Lua é menor do que a sentida no centro da Terra. Em relação ao centro da Terra, um lado está sendo puxado na direção da Lua e o outro lado está sendo puxado na direção contrária. Como a água flui muito facilmente, ela se "empilha" nos dois lados da Terra, que fica com um bojo de água na direção da Lua e outro na direção contrária. 
Figura fora de escala da Terra e da Lua Enquanto a Terra gira no seu movimento
diário, o bojo de água continua sempre apontando aproximadamente na
direção da Lua. Em um certo momento, um certo ponto da Terra estará
exatamente embaixo da Lua e terá maré alta. Seis horas mais tarde, a
rotação da Terra terá levado esse ponto a
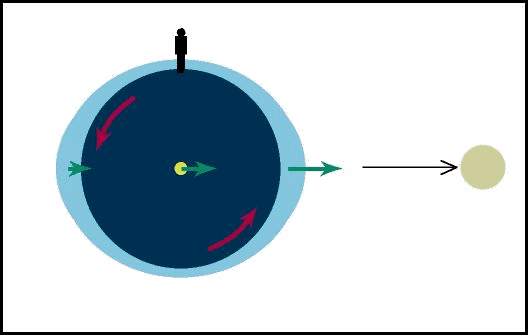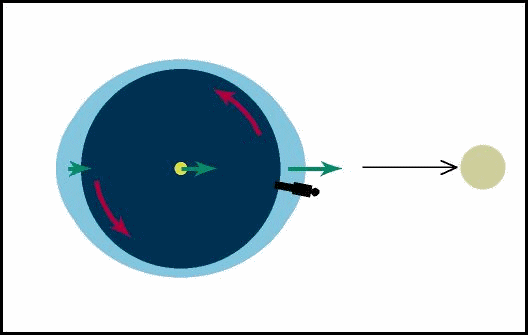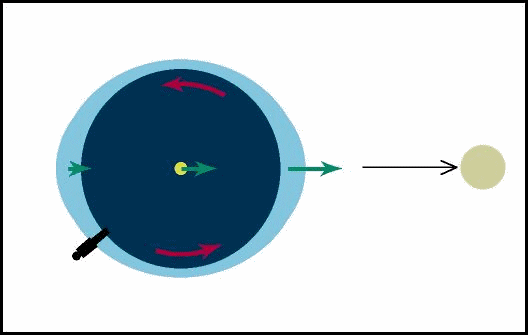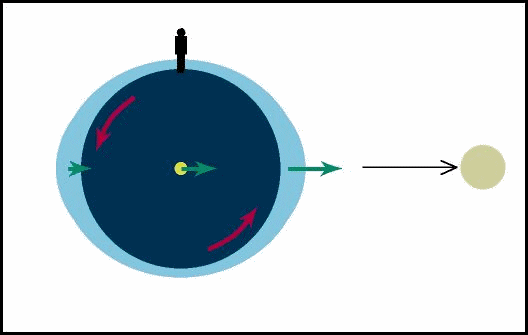 Figura fora de escala da Terra e da Lua Se a Terra fosse totalmente coberta de água, a máxima altura da maré seria 1 m. Como a Terra não é completamente coberta de água, vários aspectos resultantes da distribuição das massas continentais contribuem para que a altura e a hora da maré variem de lugar a outro. Em algumas baías e estuários as marés chegam a atingir 10 m de altura.
Fonte:http://astro.if.ufrgs.br
Conheça o Ache Tudo e Região o portal de todos Brasileiros. Coloque este portal nos seus favoritos. Cultive o hábito de ler, temos diversidade de informações úteis ao seu dispor. Seja bem vindo , gostamos de suas críticas e sugestões, elas nos ajudam a melhorar a cada ano. |
|
|
Copyright © 1999 [Ache Tudo e Região]. Todos os direitos reservado. Revisado em: 03 fevereiro, 2024. Não nos responsabilizamos pelo conteúdo expresso nas páginas de parceiros e ou anunciantes. (Privacidade e Segurança) |

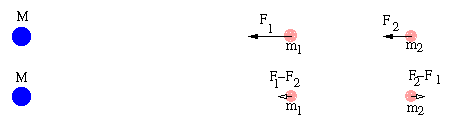
![F_1 - F_2 = GM{[\frac{m_1}{{(r-R)}^2} - \frac{m_2}{r^2}]}](gifs/img8.gif)